Delta time e sistema de coordenadas

Neste capítulo serão apresentados e implementados os elementos de controle de tempo (Delta Time) dentro do Unreal Engine, apresentaremos também o funcionamento do sistema de coordenadas dos objetos.

1. O que é Delta Time?

A simulação de movimento é realizada renderizando imagens quadro a quadro, frames, cada quadro é executado dentro de período de tempo e a diferença de tempo é chamado de Delta, por conseguinte Delta Time é o tempo entre cada frame.

Time.deltafime = 0		Tempo.DeltaTme = 0.05
Frame 1		Frame 2
	Tempo passado entre frames é 0.05

No exemplo acima verificamos que o tempo transcorrido entre o frame 1 e o frame 2 é de 0.05 milissegundos.

1.1. Frames e Delta time

Figura: Animação por quadros.

Frames	1	2	3	4	5	6	7	8	9	10
Delta	1	2	3	4	5	6	7	8	9

1.2. Calculando o FPS

Frames per Second ou quadros por segundo (FPS), é a quantidade de quadros exibidos em um segundo, para exemplificar vamos considerar a tabela anterior para calcular o FPS.

• 10 Fps = 10 frames a cada segundo;

  • 1 segundo / 9 = 0,1 segundo ou 100ms;

• 100 FPS = 100 frames a cada segundo;

  • 1 segundo /99 = 0,01 segundo ou 10ms

• 30 FPS = 1/29 , 0.034 34ms;

• 60 FPS = 1/59 , 0.017 17ms;

1.3. Utilizando comandos do console

O Unreal Engine permite visualizar e alterar os frames por segundo, FPS utilizando o console de comandos cmd.

Figura: Para habilitar o console de comandos utilizamos Menu > Project Settings > Engine Inputs ou digitar na busca a palavra console, em seguida associe uma tecla ao console, o padrão é a tecla (´).

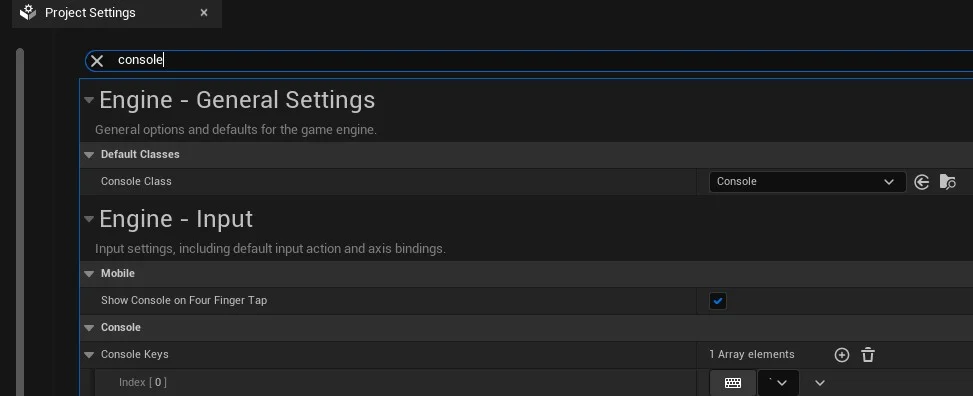
Uma vez configurado podemos voltar para a tela principal ou ViewPort para acionar o console.

Pressione a tecla ´, configurada anteriormente, e o editor de comandos aparece na tela;

1.3.1. Apresentando o valor de FPS

Figura: Comando : stat fps.

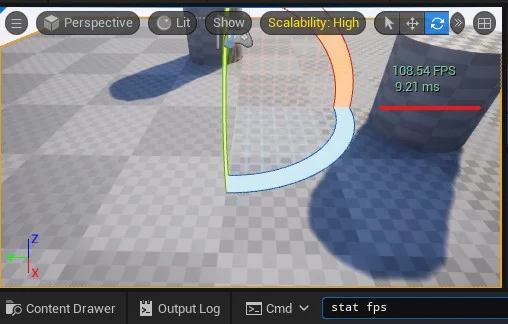
stat fps

1.3.2. Alterando o valor de FPS para 100

  t.MaxFPS 100

1.3.3. Exibindo informações de desempenho

stat unit

Valores:

• threads Frame;

• Game;

• Draw;

• GPU;

• RHIT;

• e DynRes do projeto.

Informação: Para saber mais sobre cada elemento acesse visibilidade e oclusão do curso de Computação gráfica.

1.4. Fornecendo feedback sobre quanto tempo vários Ticks de jogo estão demorando

stat game

Quanto a quantidade de ticks sendo executados e o tempo que é gasto para execução de cada um deles, o que pode ser um problema de performance do seu jogo, devemos ter em mente o seguinte:

• Considere uma cena com 500 objetos Blueprints, se a propriedade Start With Tick Enabled está habilitada o Unreal vai testar e executar cada um dos eventos, caso não seja necessário ter um tick para os blueprints é recomendável desabilitar essa propriedade.

• Os Ticks podem estar associados a loops, como por exemplo, for loop, while ou outras estruturas de repetição que consomem ciclos de CPU, caso a lógica apresente consumo elevado de CPU considere remover essas estruturas do tick e até reescrever a lógica.

Nota: Uma dica bem legal quanto ao uso de estruturas de repetição associados a Ticks, o evento Tick é um laço de repetição e pode substituir loops explicitamente, consulte o tópico “Usando o evento Tick com Blueprint” no módulo “Implementando a movimentação do personagem” para ver um exemplo do que foi falado.

1.4.1. Desabilitando o Tick

Podemos desabilitar o tick ao criar o objeto usando C++.

APlataforma::APlataforma()
{
  PrimaryActorTick.bCanEverTick = false;
  SetMobility(EComponentMobility::Movable);

}

Ou usando Blueprint selecionando o objeto na lista de Componentes e acessando a propriedade em Detalhes.

2. Delta seconds

Delta Seconds, no Unreal Engine, é a quantidade de tempo decorrido desde o último evento Tick.

Ao multiplicar o deslocamento em unidades (centímetros ou metros) de um objeto, pela variável Delta Seconds, o movimento do objeto será independente da taxa de quadros.

Por exemplo, seu peão tem uma velocidade máxima de 100 unidades por segundo. Se um segundo tivesse se passado desde o último tique de evento, seu peão moveria todas as 100 unidades. Se meio segundo tivesse passado, ele se moveria 50 unidades.

2.1. Tabela de velocidade

Distância	Velocidade	Distância/Velocidade	FPS	Delta Seconds	Y
100	10	10	100	0,1	1
100	10	10	60	0,166	1,6
100	10	10	30	0,333	3
100	10	10	20	0,5	5

Delta seconds - Intervalo entre os quadros;

Y - Deslocamento no eixo Y, aqui consideramos a quantidade de unidades que o objeto se desloca no eixo Y.

2.2. Utilizando o Delta seconds com Event Tick

Para exemplificar vamos controlar o movimento do objeto independente do FPS utilizando o evento Tick.

Figura: Utilizamos GetWorldLocation e incrementamos o valor de Y a cada Tick para atualziar SetWordLocation, atualizando a posição do objeto.

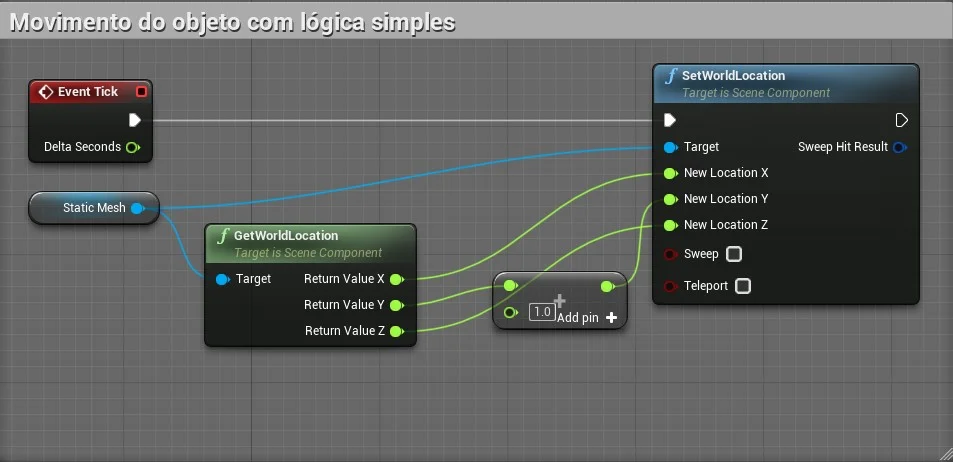
No exemplo acima se o FPS for um valor muito baixo o objeto vai se movimentar de forma lenta, por conseguinte percebemos que a movimentação será afetada pelo FPS.

Figura: Distância / Velocidade * Delta Seconds

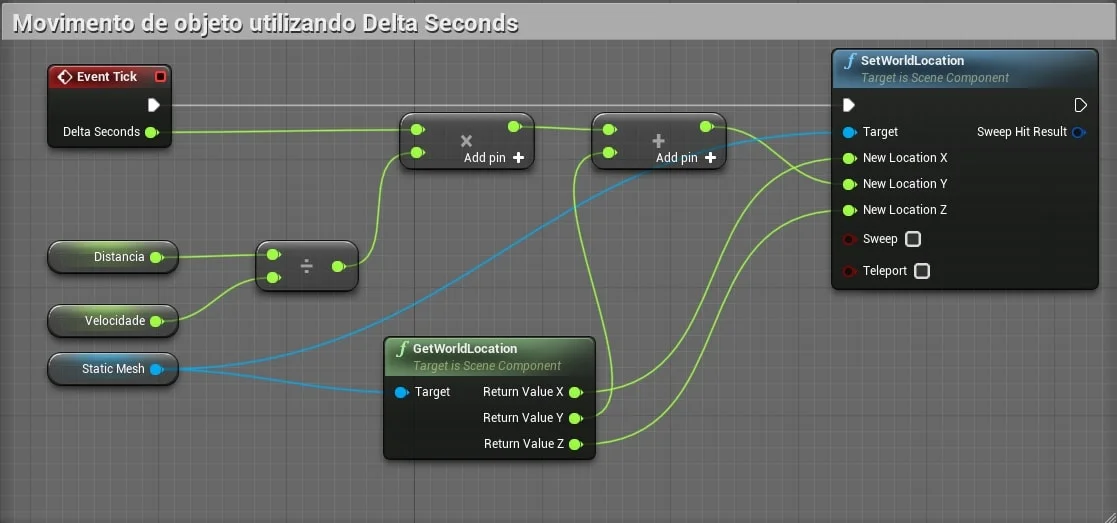
• Distancia - Valor = 1000;

• Velocidade - Valor = 10;

• O resultado esperado é que mesmo com um FPS baixo o movimento ainda se mantenha uniforme.

Quando multiplicamos o valor do Delta Seconds pela velocidade do objeto podemos ter um movimento mais fluido mesmo com valores de FPS baixos.

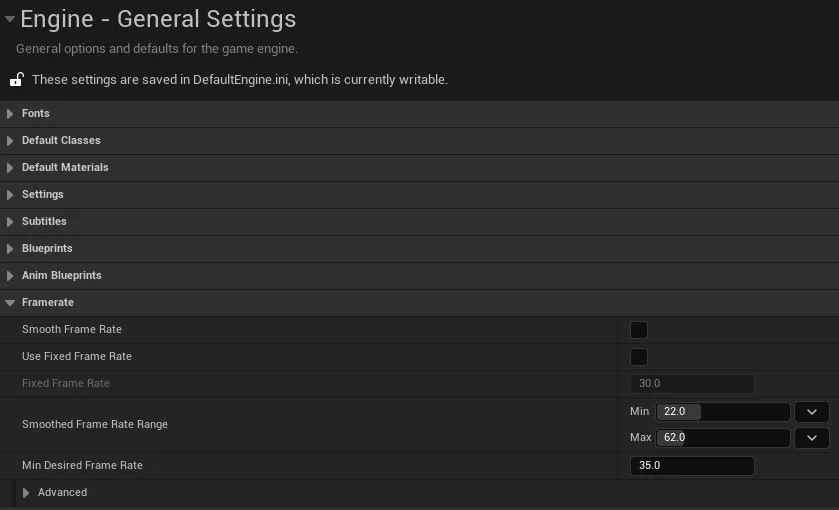
2.3. Fixando o FPS do projeto

Figura: Podemos fixar o FPS do projeto utilizando o menu Project settings > Use fixed frame rate.

2.4. Vídeo Delta Seconds e sistema de coordenadas

3. Timeline

Os nós da linha de tempo são nós especiais dentro de Blueprints que permitem que uma animação simples baseada em tempo seja projetada e reproduzida rapidamente com base em eventos no jogo. As linhas do tempo são como sequências de matinê simples, pois permitem que valores simples sejam animados e que eventos sejam disparados ao longo do tempo.

Para adicionar um objeto Timeline utilizamos Click RMB no Event Graph, lógica do objeto, e no menu de contexto selecionamos Add Timeline.

Figura: Detalhes do editor.

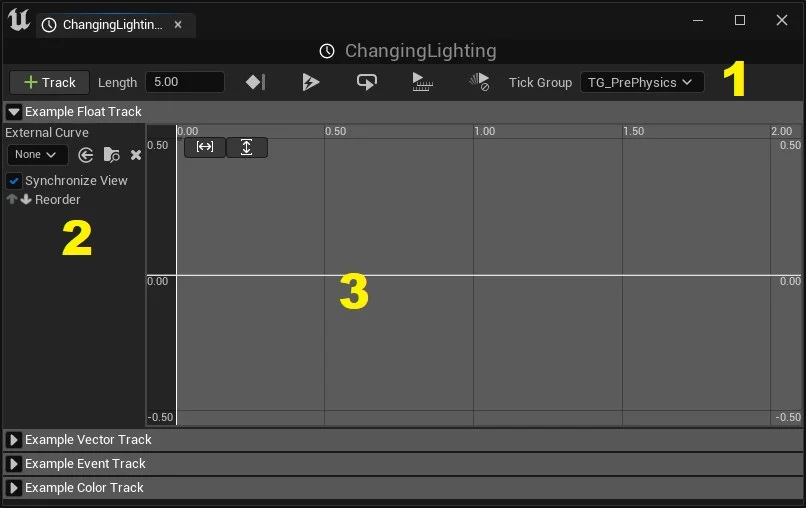
1. Parameters - Parâmetros do Timeline;

2. Trilhas externas - Permite que você escolha uma curva externa no Content Browser em vez de criar sua própria curva;

3. Trilha do Timeline - Este é o gráfico de quadro-chave para esta trilha. Você colocará quadros-chave nisso e verá a curva de interpolação resultante.

3.1. Parâmetros de entradas e saída

Figura: Nó TimeLine e suas entradas e saídas.

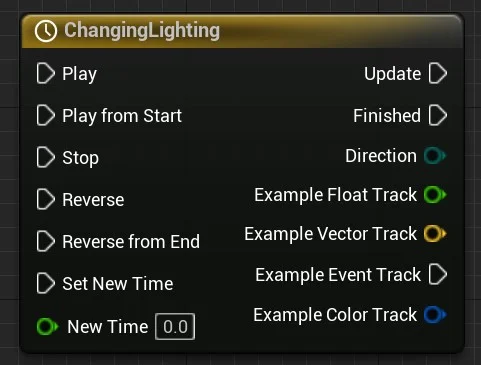
Play - Faz com que a Linha de tempo seja reproduzida a partir de sua hora atual;

Play from start - Faz com que a linha de tempo seja reproduzida desde o início;

Stop - Congela a reprodução da Linha de tempo na hora atual;

Reverse - Reproduz a linha de tempo de trás para a hora atual;

Reverse from End - Reproduz a linha do tempo de trás para frente a partir do final;

Set New Time - Define a hora atual para o valor definido (ou entrada) na entrada New Time;

New Time - Este pino de dados recebe um valor float representando o tempo em segundos, para o qual a Linha de tempo pode saltar quando a Set New Time é chamada.

3.2. Parâmetros de execução - TimeLine

Length - Permite definir a duração da reprodução para esta Linha de tempo;

Use Last KeyFrame - Se não estiver ativo, o último quadro-chave de uma sequência será ignorado. Isso pode ajudar a evitar pular quando uma animação está em loop;

Autoplay - Se ativo, este nó Timeline não requer uma entrada de execução para começar e começará a tocar assim que o nível começar;

Loop - Se estiver ativo, a animação da Linha de tempo será repetida indefinidamente, a menos que seja interrompida pelo pino de entrada Stop;

Replicated - Se ativo, a animação da Linha do tempo será replicada, pela rede, entre os clientes.

3.3. Utilizando variáveis no Timeline

Para este exemplo vamos utilizar dois objetos, um objeto Lamp do tipo Light Component para apresentar a estrutura de nó TratamentoLuz do tipo TimeLine, e outro objeto para controlar a Lamp, neste objeto utilizaremos um caixa de colisão.

A seguir vamos criar o objeto BP_ControlLight do tipo Trigger Box.

Figura: O objeto BP_ControlLight com seus componentes e variáveis.

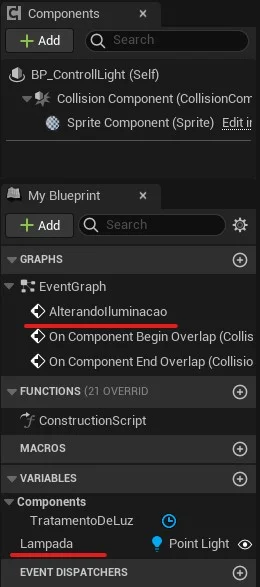
1. Adicionamos a variável Lampada do tipo PointLight e a configuramos como publica, Instance Editable para que ela possa ser acessível na janela Details do Viewport;

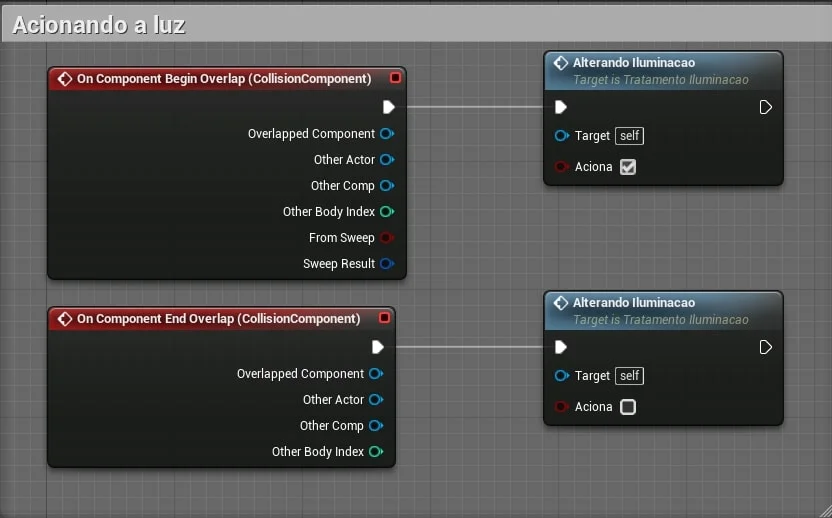
2. Adicionamos o evento customizado, Add custom event, AlterandoIluminacao.

3. Adicionamos na cena um componente PointLight e em seguida adicionamos BP_ControlLight na cena e associamos o objeto PointLight na propriedade Lamp.

Figura: Componente BP_ControlLight associando a variável Lamp ao objeto na cena.

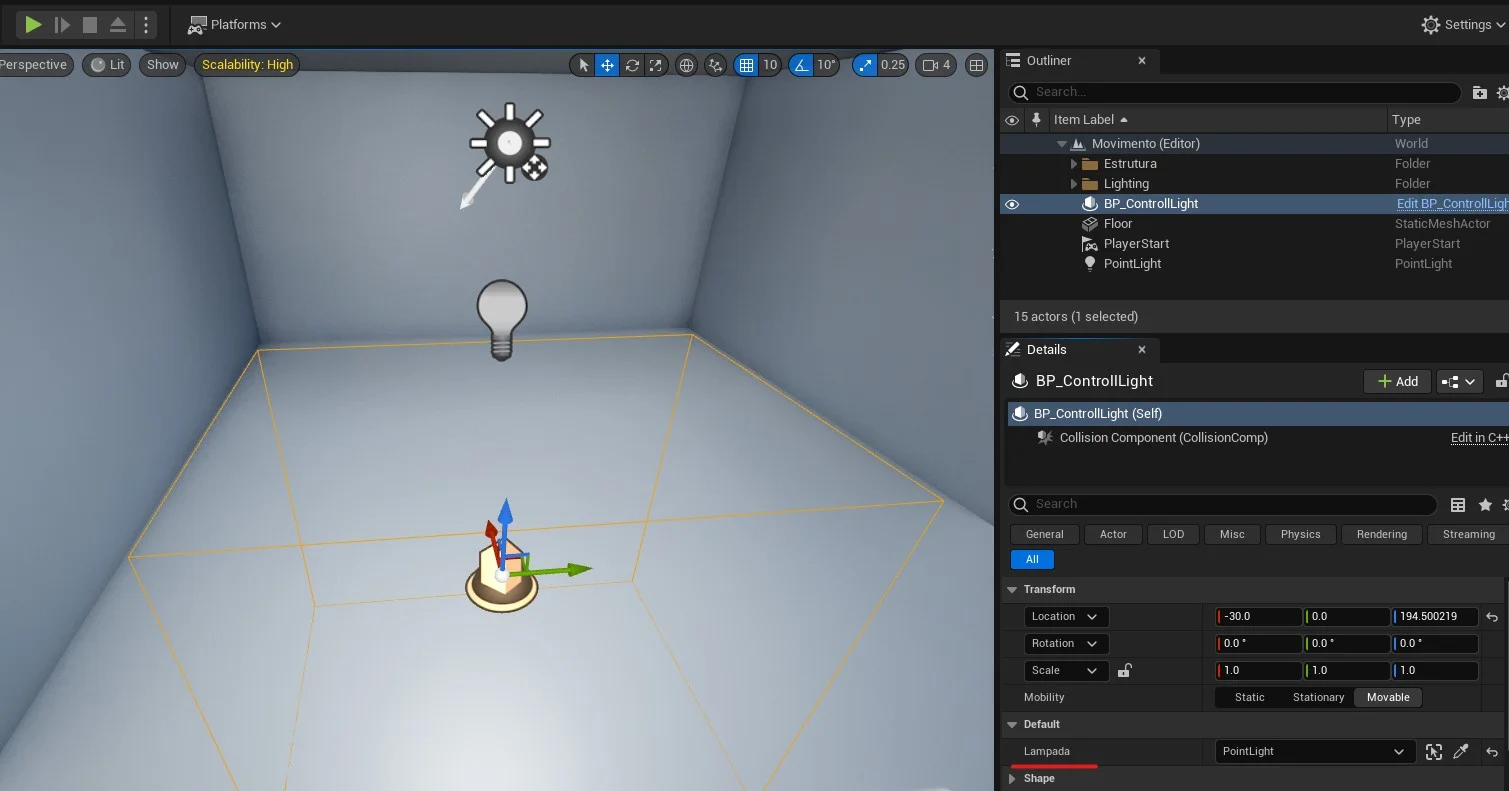
Em BP_ControlLight no Event Graph adicionamos a seguinte lógica para tratamento de luz utilizando o evento AlterandoIluminacao.

Figura: Utilizando Set Light Color, Set Intensity e TimeLine.

3.4. Tipos de variáveis do objeto TimeLine

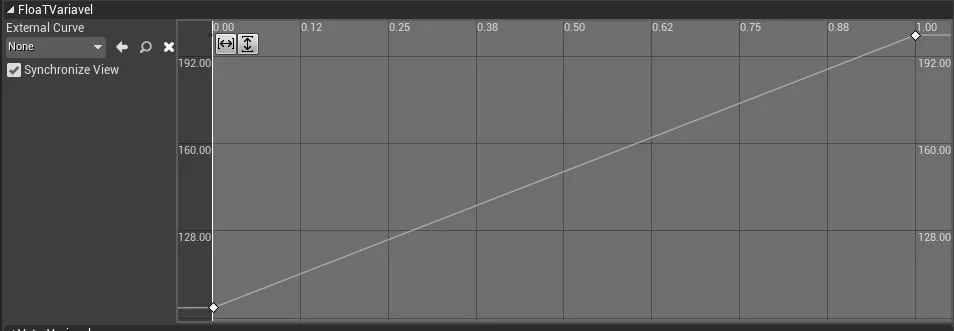
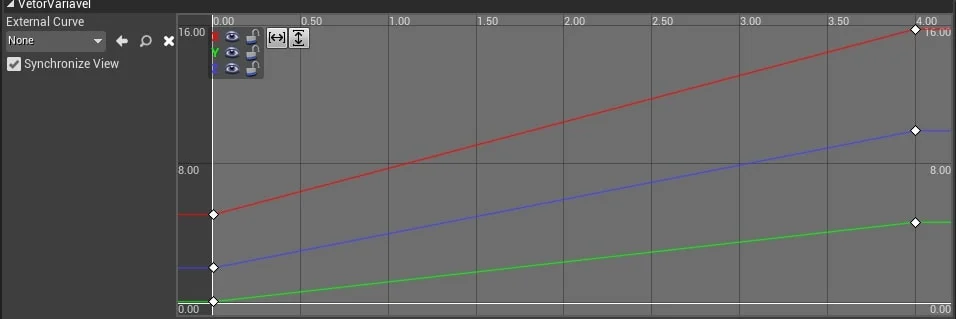
O Editor do TimeLine é um gráfico de tempo e valor, onde a linha horizontal representa os valores do tempo e a linha vertical a variação da variável.

Figura: O gráfico utiliza os tipos de dados: Float, Vector, Event e `Color`.

3.4.1. Variável float

Figura: Tipo float controla a intensidade da luz durante o tempo 1.

3.4.2. Variável Vector

Figura: Tipo Vector altera o valor das coordenadas durante o tempo 4.

3.4.3. Variável Color

Figura: Tipo Color altera as cores da luz conforme o tempo passa.

3.4.4. Variável Event

Figura: Tipo Event dispara um evento no tempo 2,4 e 6.

3.4.5. Acionando um evento para alterar a iluminação

Figura: O evento Overlap chama a função para alterar as propriedades da iluminação.

3.5. Funções Blueprint para tratamento do Timeline

• SetLooping;

• SetTimeLength;

• GetTimeLength;

• GetPlaybackPosition;

• Auto play;

• Ignore time dilation;

• Set timer by event e clear timer;

• SetTimerbyEvent;

• ClearAndInvalidateTimerByHandle;

• SetTimerbyFunction;

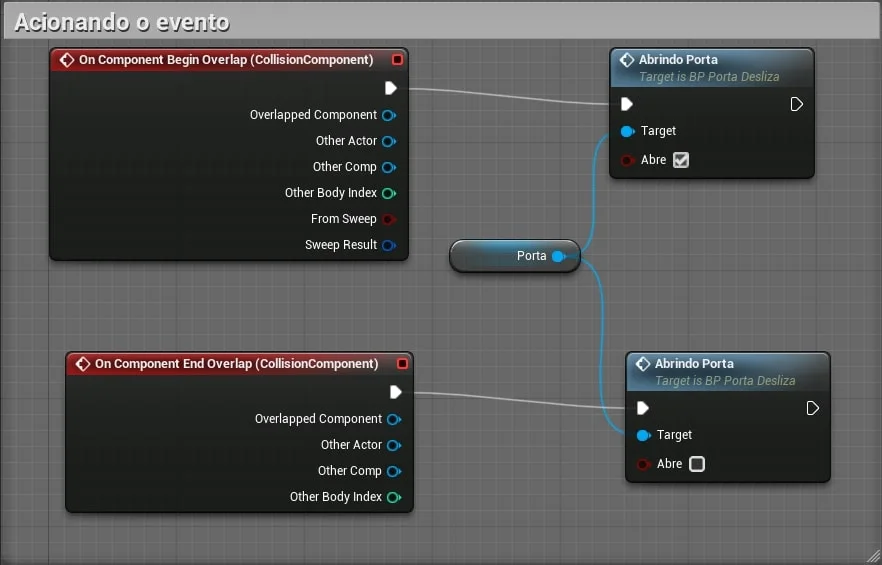
4. Abrindo portas

Nos exemplos a seguir vamos movimentar um objeto para simular a movimentação de abertura de uma porta de duas formas, deslizando e girando.

4.1. Deslizando a porta

Neste exemplo vamos implementar um movimento no eixo Y de abertura de uma porta.

Figura: Adicionando o elemento Movimentando TimeLine e alterando a posição do objeto.

Figura: Movimentando utiliza a variável Movimento do tipo `Vector`. Somente o valor de Y é alterado..

Figura: Usamos o vetor PosicaoInicial para armazenar o valor de GetActorLocations.

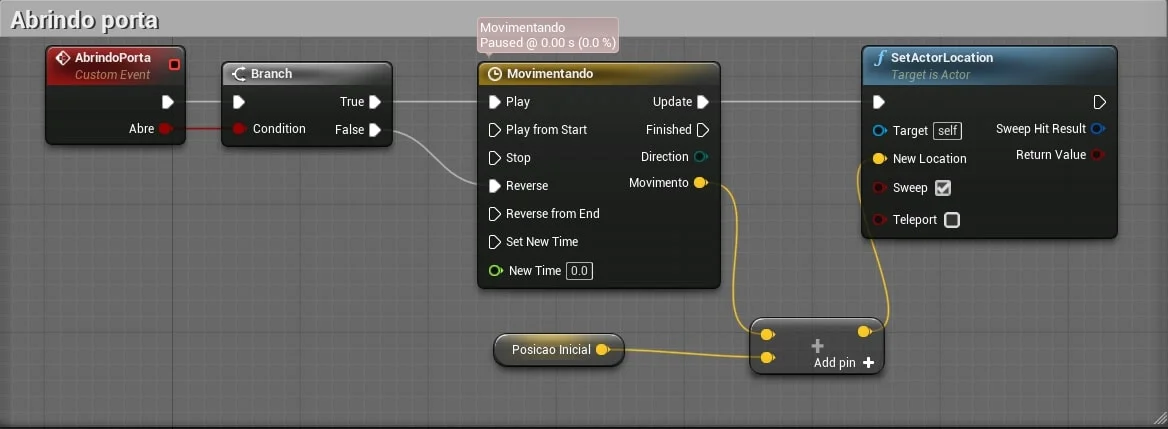
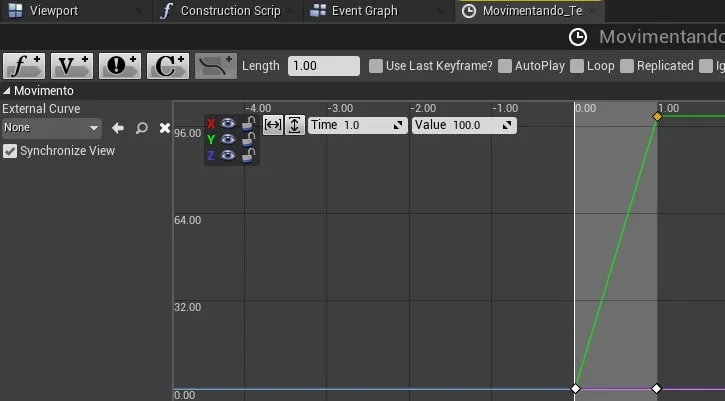
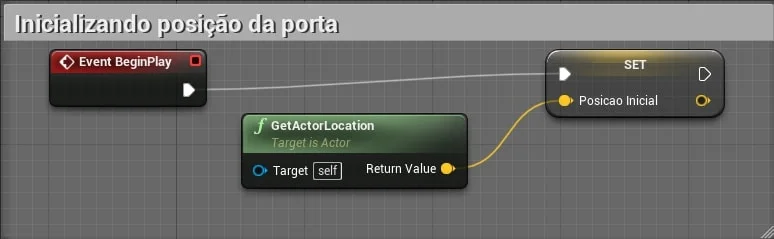
4.2. Girando a porta

Neste exemplo vamos implementar um movimento no eixo Z, girando e abrindo a porta.

Utilizamos a função MakeRotator.

Figura: Usamos somente o parâmetro Z para rotacionar o objeto. O nó Movimentando utiliza a variável *Angulo* do tipo `Vector`.

Figura: O tempo e 0 até 1 (1s) e o valor é 0 até 90 (Ângulo de rotacionamento).

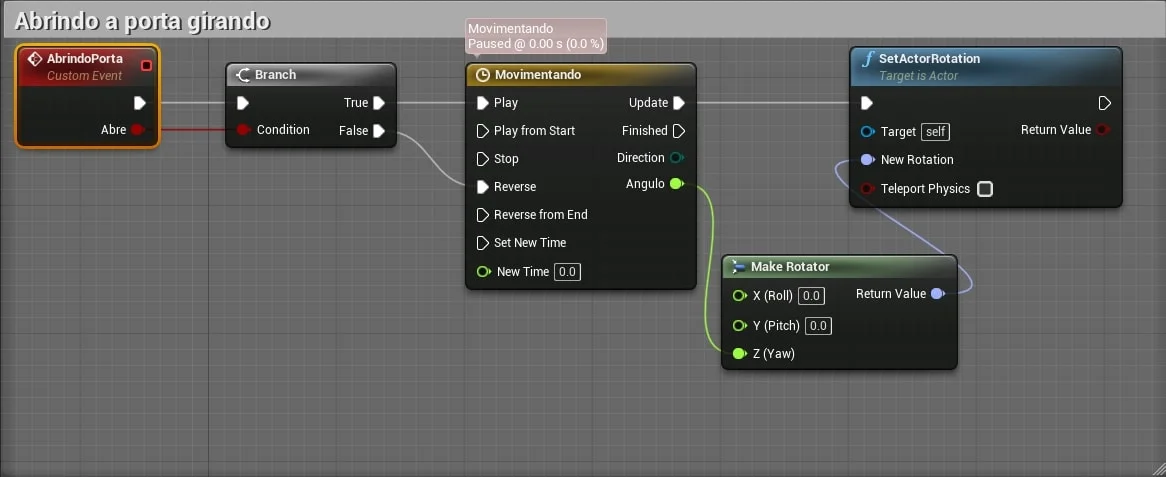
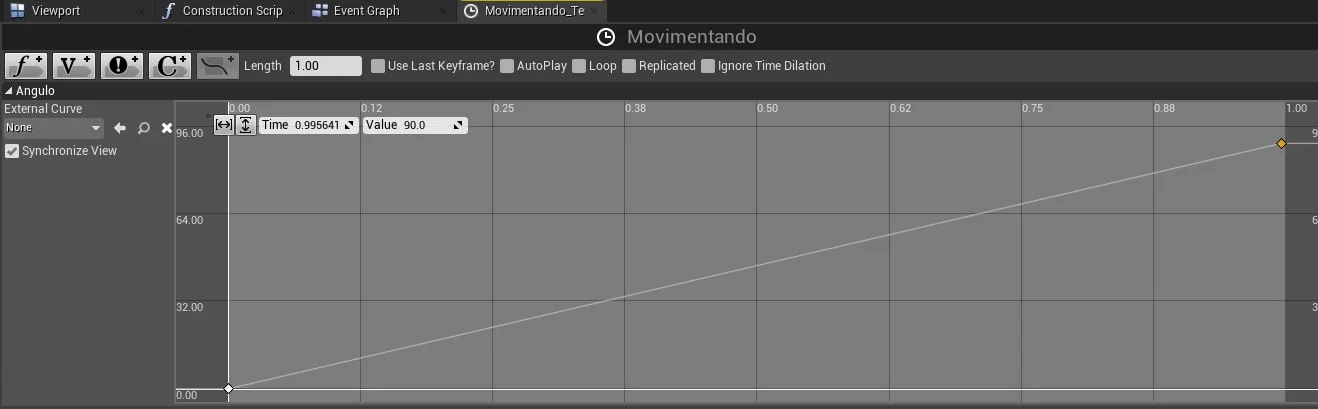
4.3. Girando a porta utilizando C++

LearpDoor.h

#pragma once

#include "CoreMinimal.h"
#include "GameFramework/Actor.h"
#include "Components/BoxComponent.h"
#include "LerpDoor.generated.h"

UCLASS()
class TCMCPP_API ALerpDoor : public AActor
{
  GENERATED_BODY()
public:

  ALerpDoor();

protected:
  virtual void BeginPlay() override;

public:
  virtual void Tick(float DeltaTime) override;

  UPROPERTY(EditAnyWhere)
  UStaticMeshComponent* MyDoor;

  UPROPERTY(EditAnywhere)
  UBoxComponent* BoxComp;

  UFUNCTION()
    void OnOverlapBegin(class UPrimitiveComponent* OverlappedComp, class AActor* OtherActor, class UPrimitiveComponent* OtherComp, int32 OtherBodyIndex, bool bFromSweep, const FHitResult& SweepResult);
  
  UFUNCTION()
  void OnOverlapEnd(class UPrimitiveComponent* OverlappedComp, class AActor* OtherActor, class UPrimitiveComponent* OtherComp, int32 OtherBodyIndex);

  bool Open;
  float RotateValue;
  FRotator DoorRotation;
};

LearpDoor.cpp

#include "LerpDoor.h"
#include "Kismet/KismetMathLibrary.h"
#include "Components/BoxComponent.h"

ALerpDoor::ALerpDoor()
{
  PrimaryActorTick.bCanEverTick = true;

  Open = false;

  BoxComp = CreateDefaultSubobject<UBoxComponent>(TEXT("My Box"));
  BoxComp->InitBoxExtent(FVector(50.0f, 50.0f, 50.0f));
  RootComponent = BoxComp;

  MyDoor = CreateDefaultSubobject<UStaticMeshComponent>(TEXT("My Door"));
  MyDoor->SetRelativeLocation(FVector(0.0f, 50.0f, -50.0f));
  MyDoor->SetupAttachment(RootComponent);

  BoxComp->OnComponentBeginOverlap.AddDynamic(this, &ALerpDoor::OnOverlapBegin);
  BoxComp->OnComponentEndOverlap.AddDynamic(this, &ALerpDoor::OnOverlapEnd);
}

void ALerpDoor::BeginPlay()
{
  Super::BeginPlay();
}

void ALerpDoor::Tick(float DeltaTime)
{
  Super::Tick(DeltaTime);

  DoorRotation = MyDoor->GetRelativeRotation();

  if (Open)
  {
    MyDoor->SetRelativeRotation(FMath::Lerp(FQuat(DoorRotation), FQuat(FRotator(0.0f, RotateValue, 0.0f)),0.01));
  }
  else
  {
    MyDoor->SetRelativeRotation(FMath::Lerp(FQuat(DoorRotation), FQuat(FRotator(0.0f, 0.0f, 0.0f)), 0.01));
  }
}

void ALerpDoor::OnOverlapBegin(class UPrimitiveComponent* OverlappedComp, class AActor* OtherActor, class UPrimitiveComponent* OtherComp, int32 OtherBodyIndex, bool bFromSweep, const FHitResult& SweepResult)
{

  if ((OtherActor != nullptr) && (OtherActor!= this) && (OtherComp != nullptr))
  {
    FVector PawnLocation = OtherActor->GetActorLocation();
    FVector Direction = GetActorLocation() - PawnLocation;
    Direction = UKismetMathLibrary::LessLess_VectorRotator(Direction, GetActorRotation());
    if (Direction.X > 0.0f)
    {
      RotateValue = 90.0f;
    }
    else
    {
      RotateValue = -90.0f;
    }
    Open = true;
}
}

void ALerpDoor::OnOverlapEnd(class UPrimitiveComponent* OverlappedComp, class AActor* OtherActor, class UPrimitiveComponent* OtherComp, int32 OtherBodyIndex)
{
  if ((OtherActor != nullptr) && (OtherActor != this) && (OtherComp != nullptr))
  {
    Open = false;
  }

}

Acionando a porta.

Figura: Ao colidir com o objeto a porta a movimentação da porta é acionada.

5. Curves

Podemos criar um tipo de objeto Curve para que possamos utilizar em vários Blueprints e determinar a variação dos valores.

Figura: Para criar um objeto do tipo Curve utilizamos o menu de contexto Miscellaneous > Curve, para o exemplo a seguir utilize uma curva do tipo Float e use o nome C_TempoPorta..

Figura: Adicionamos duas chaves ou variáveis aa Objeto C_TempoPorta.

Figura: Associamos o objeto C_TempoPorta ao objeto Movimentando de tipo Timeline.

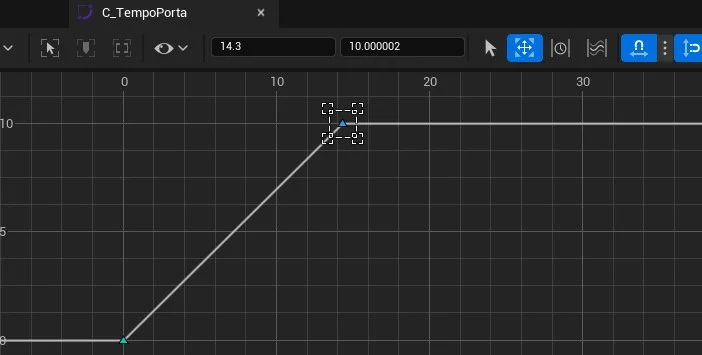
• SetVectorCurve;

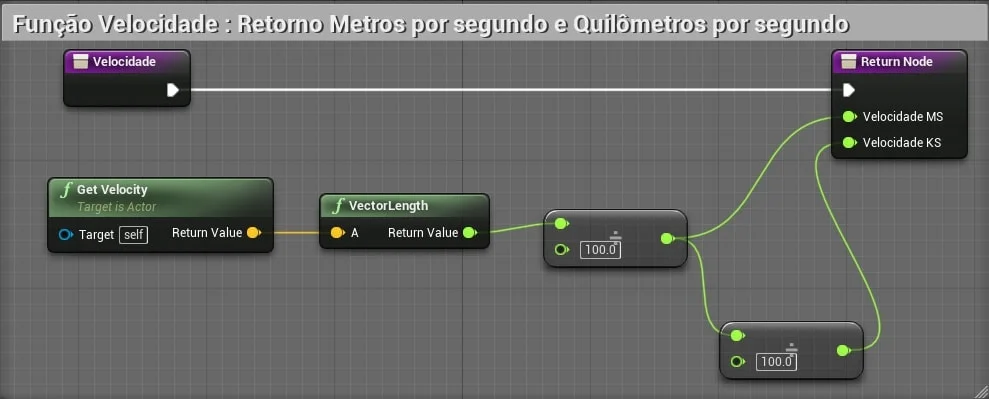
6. Exemplo de calculo de velocidade

Figura: Usamos VectorLength para obter o valor do deslocamento.

7. Sistema de coordenadas

O sistema de coordenadas descreve uma maneira de usar números para especificar a localização de um ponto (ou pontos) no espaço 2D ou 3D. Em um motor de jogo, é função do sistema de coordenadas define a localização de cada objeto e para qual direção ele está voltado. Com esses dados podemos calcular a distância entre objetos, rotação, velocidade e todos os tipos de outras informações úteis.

7.1. Plano Cartesiano

Para demonstrar vamos utilizar um vetor de 2D (x,y).

					(Y)
					5				D
					4
			B		3
					2			C
					1
-5	-4	-3	-2	-1	0	1	2	3	4	5	(X)
					-1
					-2
					-3
	A				-4
					-5

Consideramos o posição dos objetos com a seguinte expressão v = v(x,y), por conseguinte os valores para A,B,C e D são:

• A = a(-4,-4)

• B = b(-2,3)

• C = b(3,2)

• D = b(4,5)

Quanto a direção do movimento, consideramos que uma direção nos diz como nos mover no sistema de coordenadas x, y. Um valor positivo nos diz para nos movermos na direção positiva e um valor negativo nos diz para nos movermos na direção negativa (com base no sistema de coordenadas).

B = b(-2,3) -> b(-1,4)

7.2. Magnitude

A Magnitude nos diz o quanto nos movemos. A distância de um movimento provará ser muito útil e pode ser calculada apenas com o vetor. Isso é feito usando o Teorema de Pitágoras.

Assuma um objeto na posição (50, 25) e queremos movê-lo para (53, 23). Isso significa um Vetor de (3, -2).

A = a(-4,-4) -> a(2,-1)

O objeto se deslocou de (-4,-4) até a nova posição (2,1), andou 6 posições em X e 5 em Y, logo a direção de A é (6,5).

Por conseguinte a distância percorrida é :

raiz_quadrada(6 ^ 2 + 5 ^2) = 7.8

Informação: Você pode usar isso para calcular novas posições e movimentos. Suponha que você tenha um objeto na posição (12, 4) e deseja movê-lo na direção (3,2), mas deseja que a distância seja 4 vezes a distância normal. Para fazer isso funcionar e obter a nova posição, você multiplica o vetor pelo escalar V = (34,24) (12,8) A nova posição no sistema de coordenadas x / y é obtida adicionando este vetor para a posição original: (12 + 12, 4 + 8) (24, 12)

7.3. Normalização

Aprendemos que um vetor é um par de números que contém uma direção e que pode ser usado para derivar uma magnitude. Quando um vetor contém um par de números, como (10, 5), ele indica que o movimento será de 10 unidades na direção X positiva e 5 unidades na direção Y positiva. Este vetor especifica quantas unidades mover, mas também indica uma direção geral em porcentagens. Essa é a proporção de movimento de 10 por 5. O cálculo dessa porcentagem de movimento é chamado de Normalização de um vetor.
O vetor normalizado é um par de números, cada um deles menor que um. Você pode criar um vetor normalizado obtendo a magnitude de um vetor e dividindo cada valor do Vetor pela magnitude. Com um vetor de (3,4) a magnitude é 5.

5 = raiz_quadrada(3 ^ 2 + 4 ^2)

(.6,.8) = (3/5, 4/5)

Resultado: O vetor normalizado das coordenadas (3,4) é (-.6,.8).

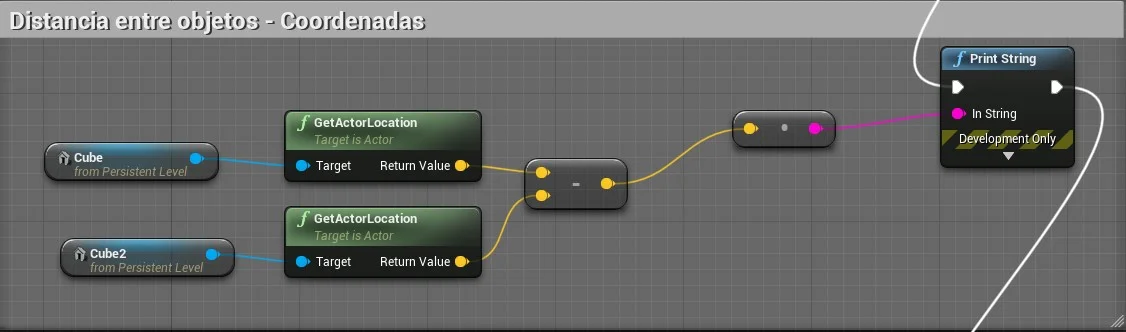
8. Calculando distância

Usando a função GetActorLocation podemos determinar a distância entre dois objetos, no exemplo a seguir vamos calcular a distância dos objetos Cube e Cube2 .

• Cube - a=GetActorLocation(0,-600,70)

• Cube2 - b=GetActorLocation(600,600,70)

• Resultado - Resultado = a - b

  (600,1200,0)

Consideramos a diferença de localização dos objetos e objetos o valor usando VectorLength para transformar em um valor do tipo float.

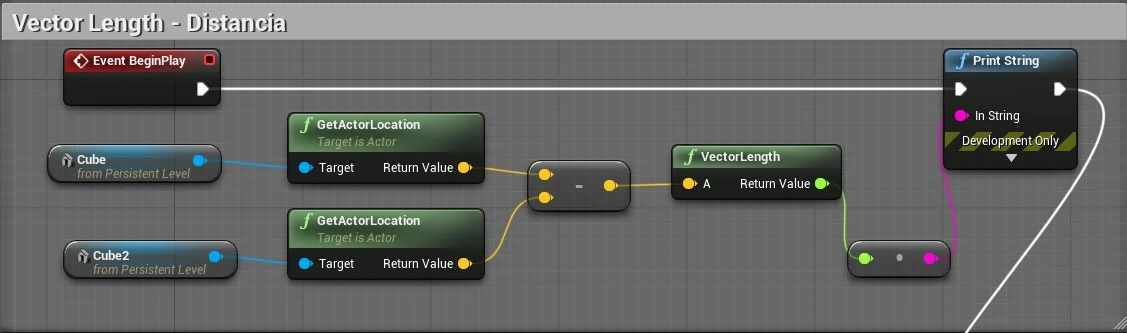
8.1. VectorLength

Figura: Calcula o comprimento do vetor, onde Comprimento = VectorLength(Resultado) (1341.64078).

8.2. GetDistanceTo

Calcula a distância de dois objetos, onde Distancia = GetDistanceTo(Cubo,Cubo2) (1341.64078).

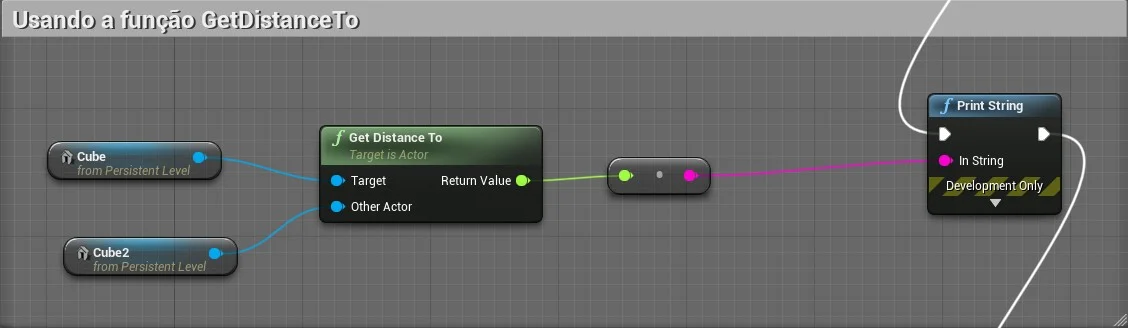
8.3. Normalize

a = Cubo.GetActorLocation(0,-600,70)

Resultado = Normalize(a,0)

(0,0.99,0.16)

Os valores variam entre 0 e 1.

Figura: O nó retorna um vetor normalizado.

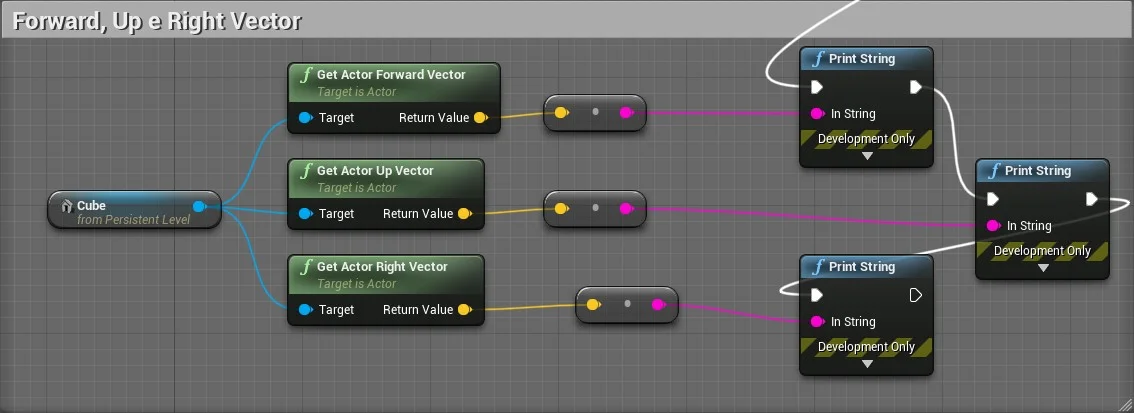
9. Verificando para onde o ator está apontando

Usaremos várias funções para verificar a direção que o ator está apontando.

• GetActorForwardVector

  a = Cubo.GetActorForwardVector()

  1,0,0

• GetActorUpVector
  a = Cubo.GetActorUpVector()

  0,0,1

• GetActorRightVector
  a = Cubo.GetActorRightVector()

  0,1,0

Figura: Definir onde o ator esta apontando.

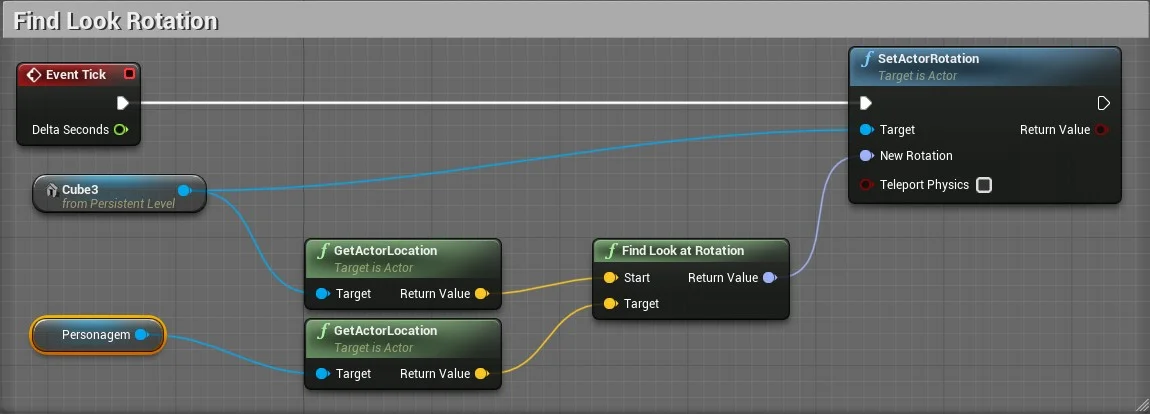
10. Acompanhando o movimento de um objeto

Usaremos a função FindLookAtRotation para que um objeto se movimente no seu próprio eixo baseado na posição de outro objeto, no exemplo o Cubo3 do tipo Character vai apontar para a face de outro objeto.

Figura: Atualizamos a posição do Personagem para usar como referência em FindLookRotation.